hakid29

이 글에서는 interactive ZKP와 non-interactive ZKP가 무엇인지와 그 예시에 대하여 알아본다.


Interactive proof system이란 prover와 verifier 사이의 정보를 교환하는 computation을 모델링한 이론적인 컴퓨팅 모델이다. Interactive proof에서는 prover가 infinite computing power을, verifier은 제한된 computing power을 가지고 있으므로 주로 prover가 dishonest한 경우를 가정하고 공격 시나리오를 생각한다.

하지만 verifier가 dishonest한 경우를 고려하기 시작하면서 ZKP가 등장하였다.

Property of ZKP

ZKP는 항상 다음과 같은 조건을 모두 만족시켜야 한다.

• Completeness : honest prover가 secret을 알고 있다면 honest verifier은 이를 납득할 수 있다.
• Soundness : honest verifier가 납득한다면 prover은 secret을 알고 있는 것이다. 즉, prover가 secret을 모른다면 verifier을 납득시킬 수 없다.
• Zero-knowledgeness : dishonest verifier는 secret에 대한 그 어느 정보도 알 수 없다.

Fiat-Shamir protocol

Interactive ZKP의 대표적인 예시인 Fiat-Shamir protocol을 알아보자.


Goal
$v$와 큰 소수 2개의 곱으로 이루어진 $n$에 대하여 $v = s^2 \ (mod \ n)$을 만족하는 $s$가 존재함을 prover가 verifier에게 납득시키려 한다.


setup
private input는 prover만 알고 있고, public input는 prover와 verifier 모두가 알고 있는 정보이다.

• private input : $s$
• public input : $n$, 그리고 $v = s^2 \ (mod \ n)$를 만족하는 $v$

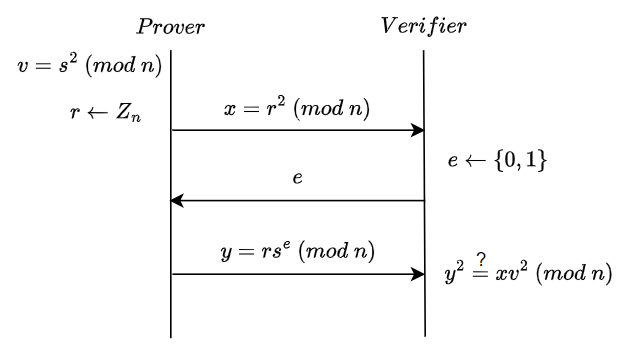
1. Commitment : Prover은 random한 수 $r$을 골라 verifier에게 $r$에 대한 commitment $x$를 전달한다.
2. Challenge : Verifier은 prover에게 0 또는 1을 challenge값으로 전달한다.
3. Response : Prover은 verifier에게 $y$를 전달한다.
4. Verification : Verifier은 $y^2 = xv^e \ (mod \ n)$을 만족하는지 확인한다.

위의 과정을 여러 번 반복하면 malicious prover가 verification을 모두 통과할 가능성이 적어진다.

• Completeness
  $e=0 \rightarrow y = r, y^2 = r^2 = x = xv^0 \ (mod \ n)$
  $e=1 \rightarrow y = rs \ (mod \ n), y^2 = r^2s^2 = xv^1 \ (mod \ n)$
• Soundness
  $e=1 \rightarrow$ $x = \frac{r^2}{v}$로 Commitment에서 보냄
  $y=r$로 response하면 verification통과, 즉, 50%확률로 verifier의 $e$를 예상하여 통과 가능
  여러 번 반복하므로 soundness도 만족
• Zero-knowledgeness
  원래는 simulator을 생성하여 얻을 수 있는 정보와 실제를 비교하여 같음을 증명해야 하지만 brief하게 설명하자면 verifier은 $s$에 대한 어느 정보도 얻지 못하므로 만족

Interactive ZKP의 경우, prover와 verifier가 항상 on-line상태여야 하고 연산을 반복해야 하므로 비효율적이라는 단점이 있다. 그래서 나온게 non-interactive ZKP이다.

Schnorr identification protocol

Non-interactive ZKP의 예시인 Schnorr identification protocol을 알아보자.


Non-interactive는 prover와 verifier의 정보 교환이 최소화되는 것이 핵심이다. prover은 verifier에게 증명에 필요한 정보를 주기만 하고 받지는 않는다.


Goal
소수 $p$에 대하여 $h = g^x \ (mod \ p)$를 만족하는 $x$를 알고 있음을 prover가 verifier에게 납득시키려 한다.


setup

• private input : $x$
• public input : $p$, $g$, $h$, 그리고 $q \ | \ p-1$, $g^q=1 \ (mod \ p)$를 만족하는 $q$

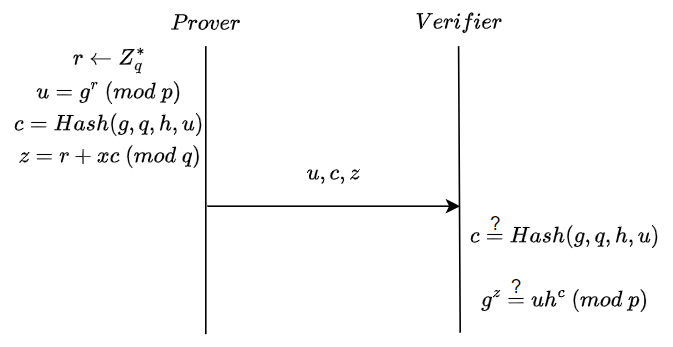
• Completeness
  $g^z = g^{r+xc} = uh^c \ (mod \ p)$
• Soundness
  $u$가 확정되면 $c$도 확정되므로 그에 맞는 $z$를 찾기 위해서는 dlp를 풀어야한다. 따라서 $x$를 모르면서 $g^z=uh^c \ (mod \ p)$를 만족하는 $(u,c,z)$를 찾을 확률은 negligible하다.
• Zero-knowledgeness
  verifier은 $x$에 대한 어느 정보도 얻지 못하므로 만족

Non-inveractive ZKP에서 succinctness((간결함)), 즉, proof size를 줄이고 빠르게 verify를 할 수 있도록 하여 실용성을 극대화시킨 것이 zk-SNARKs라고 한다. 이는 차차 공부해보자.