Lindell17 protocol은 2017년 Lindell에 의해 개발되었으며 대표적인 MPC 중 하나이다. Lindell17 protocol에서는 two parties가 ECDSA key의 분리된 share을 생성하고 두 party가 모두 message를 sign하고 싶을 때에만 sign할 수 있다.
Practical Key-Extraction Attacks in Leading MPC Wallets 를 기반으로 Lindell17 protocol과 이에 대한 broken record attack을 소개하겠다.
Lindell17 protocol에 쓰이는 Paillier Encryption을 먼저 살펴보자.
Paillier Encryption
$p, q$ : 1024 bit prime
public key : $N = pq$
private key : $σ=(p-1)(q-1)$
Encryption
message $m ∈ Z_n$, random number $ρ∈Z_N^* $
$$Enc_N(m;ρ) = (1 + N)^mρ^N \ (mod \ N^2)$$
Decryption
ciphertext $C∈Z_{N^2}^* $, $µ = σ^{-1} \ (mod \ N)$
$$
Dec_σ(C) = (\frac{C^σ \ (mod \ N^2) -1}{N})µ \ (mod \ N)$$
$$= (\frac{(1 + N)^{mσ} \ (mod \ N^2) - 1}{N})µ \ (mod \ N) \ \ \ (\because ρ^{Nσ} = 1 \ (mod \ N^2))$$
$$= (\frac{1 + mσN - 1}{N})µ \ (mod \ N)$$
$$= (mσ)µ \ (mod \ N)$$
$$=m \ (mod \ N)$$
Lindell17 protocol
KeyGen
Alice와 Bob이 group-generator-order tuple $(G, g, q)$을 생성하고 $x_A, x_B ∈Z_q$에 대하여 다음과 같이 key를 생성한다.
$$ (N, σ) \leftarrow PailKeys \ \ and \ \ X=g^{x_A + x_B}, C \leftarrow Enc_N(x_B) $$
*여기서 $G$는 타원곡선 점들의 집합, $g$는 타원곡선의 generator, $q$는 타원곡선의 order을 말하는 것으로 보인다.즉, $g^k$는 $k$와 generator을 곱한 점의 $x$좌표를 말한다.
public key : $X∈G$, $N∈Z$
Alice's private key : $x_A$
Bob's private key : $x_B, σ$
또한, $C$가 Alice에게 전달된다.
Protocol
*MulShare은 $k_A, k_B$를 주면 $R = g^{k_Ak_B}$를 주는 oracle이다.

*operation 4에 $k_2^{-1}Dec_σ(C)$가 아니라 $k_B^{-1}Dec_σ(D)$인 것 같다.
Operation 자체는 꽤 단순하다.
4 부분만 보자.
$$s = k_B^{-1}Dec_σ(D) \ (mod \ q)$$
$$ = k_B^{-1}Dec_σ(Enc_N(k_A^{-1}(m+rx_A) \ (mod \ q))Enc_N(x_Brk_A^{-1} \ (mod \ q))) \ (mod q)$$
$$ = k_B^{-1}Dec_σ(Enc_N(k_A^{-1}(m+rx_A )+ x_Brk_A^{-1} \ (mod \ q)) \ (mod q) $$
$$(\because paillier \ encryption \ is \ additively \ homomorphic)$$
$$ = k_B^{-1}k_A^{-1}(m + r(x_A + x_B)) \ (mod \ q)$$
위 과정으로 인해 Bob은 Alice로부터 $D$를 받아 valid signature인 $s$를 계산할 수 있다.
결론적으로 Alice와 Bob은 message $m$에 대한 서명 $r, s$를 protocol을 통해 생성할 수 있다.
Broken Record Attack

Bob은 $x_B - y_B \ (mod \ 2^l) = 0$ 인 경우에만 signature을 올바르게 생성할 수 있다. 따라서 Alice(attacker)는 $l$을 1씩 늘려가며 Bob의 response에 따라 $x_B$의 lsb를 하나씩 leak할 수 있다.
Proof
Alice가 $k_A = 2^l$로 고른다면 $s = (2^lk_B)^{-1}(m+r(x_A+x_B)) \ (mod \ q)$ 가 된다.
$\zeta = 2^{-l}(m+rx_A) \ (mod \ q), \zeta' = y_Br'2^{-l} \ (mod \ q)$라 하면
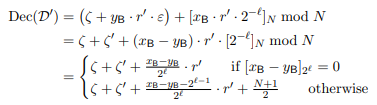
)
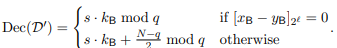
위와 같은 과정을 통해 증명이 된다.
혹여나 Broken record attack 관련 wargame을 풀고 싶다면 DownUnderCTF2024에 출제된 super party computation을 풀어보길 바란다. CVE-2023-33242기반의 문제이며 이 문제의 Mulshare oracle에서 $x_A+x_B$가 아닌 $x_Ax_B$로 계산하지만 공격 자체는 완벽히 동일하게 통한다.